1. 🎯 Definición y Propósito
Un modelo matemático es una «traducción» de un fenómeno real (como la demanda de un producto o la velocidad de un objeto) a una descripción matemática.
Su objetivo principal no es solo describir, sino comprender el fenómeno y, lo más importante, hacer predicciones sobre su comportamiento futuro.
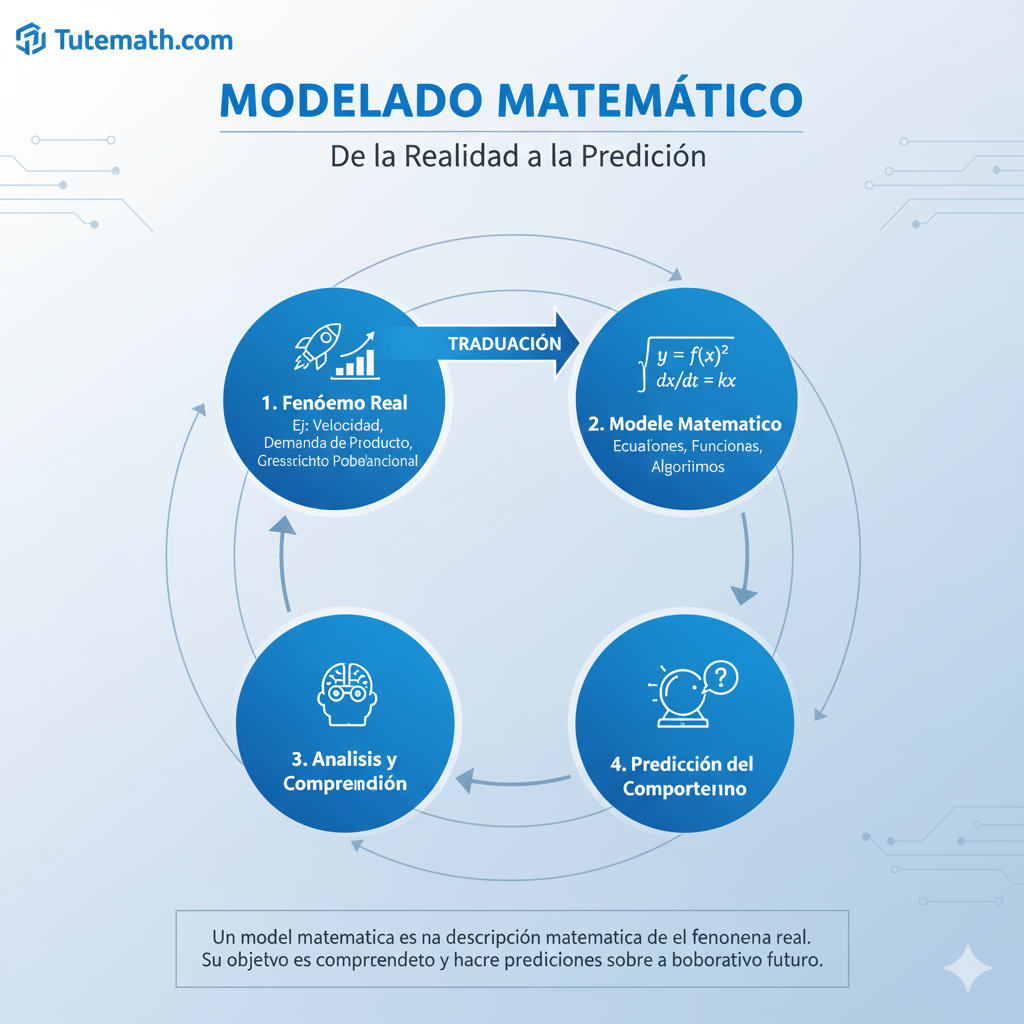
2. 🔄 El Proceso Cíclico del Modelado
Este proceso comprende 4 etapas como son:
- Formulación: Este es el primer paso y el más crucial. Implica:
- Identificar las variables (dependientes e independientes).
- Hacer supuestos para simplificar la realidad y hacerla manejable.
- Usar leyes físicas conocidas o, si no hay, recolectar datos (tablas, gráficos) para encontrar patrones y formular ecuaciones que relacionen las variables.
- Análisis Matemático: Una vez que se tiene el modelo (la ecuación o función), se aplican herramientas matemáticas (como el Cálculo) para resolverlo y obtener conclusiones matemáticas.
- Interpretación: Las conclusiones matemáticas (los resultados de las ecuaciones) se «traducen» de nuevo al mundo real. Se convierten en explicaciones o predicciones sobre el fenómeno original.
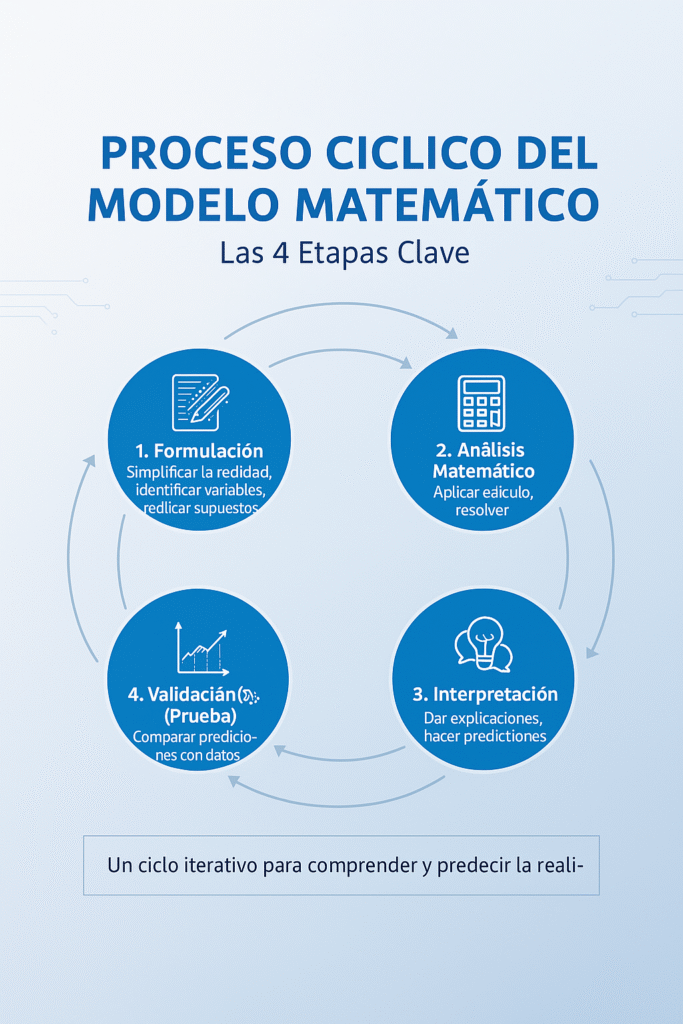
4. Validación (Prueba): Este es el paso final y el que cierra el ciclo. Las predicciones del modelo se comparan con nuevos datos reales.
- Si las predicciones coinciden bien con la realidad, el modelo es útil.
- Si no coinciden, el modelo debe ser refinado (ajustando los supuestos) o descartado, y el ciclo comienza de nuevo.
3. ⚠️ La Naturaleza y Limitaciones de un Modelo
Un punto fundamental: un modelo matemático nunca es una representación 100% precisa de la realidad. Siempre es una idealización.
- Un buen modelo no es el más complejo, sino el que logra un equilibrio: simplifica la realidad lo suficiente para poder hacer cálculos, pero se mantiene lo bastante preciso para dar conclusiones valiosas y útiles.
- Es crucial que el modelador (el científico o ingeniero) comprenda las limitaciones de su propio modelo.

De forma concluyente se puede señalar que existen muchos tipos de funciones (lineales, polinómicas, exponenciales, etc.) que sirven como herramientas para modelar las diferentes relaciones que se observan en el mundo real, y que estas serán analizadas en detalle más adelante.
