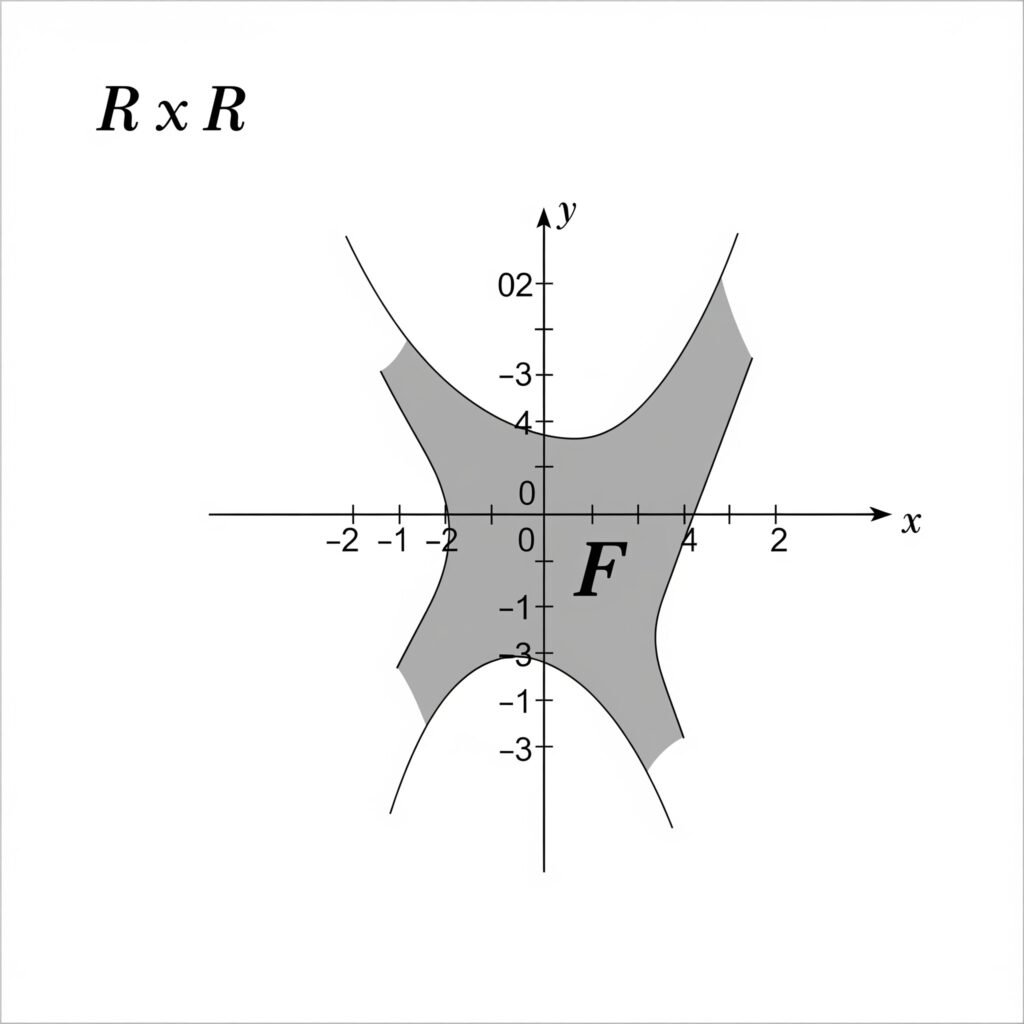
Descripción de las Funciones
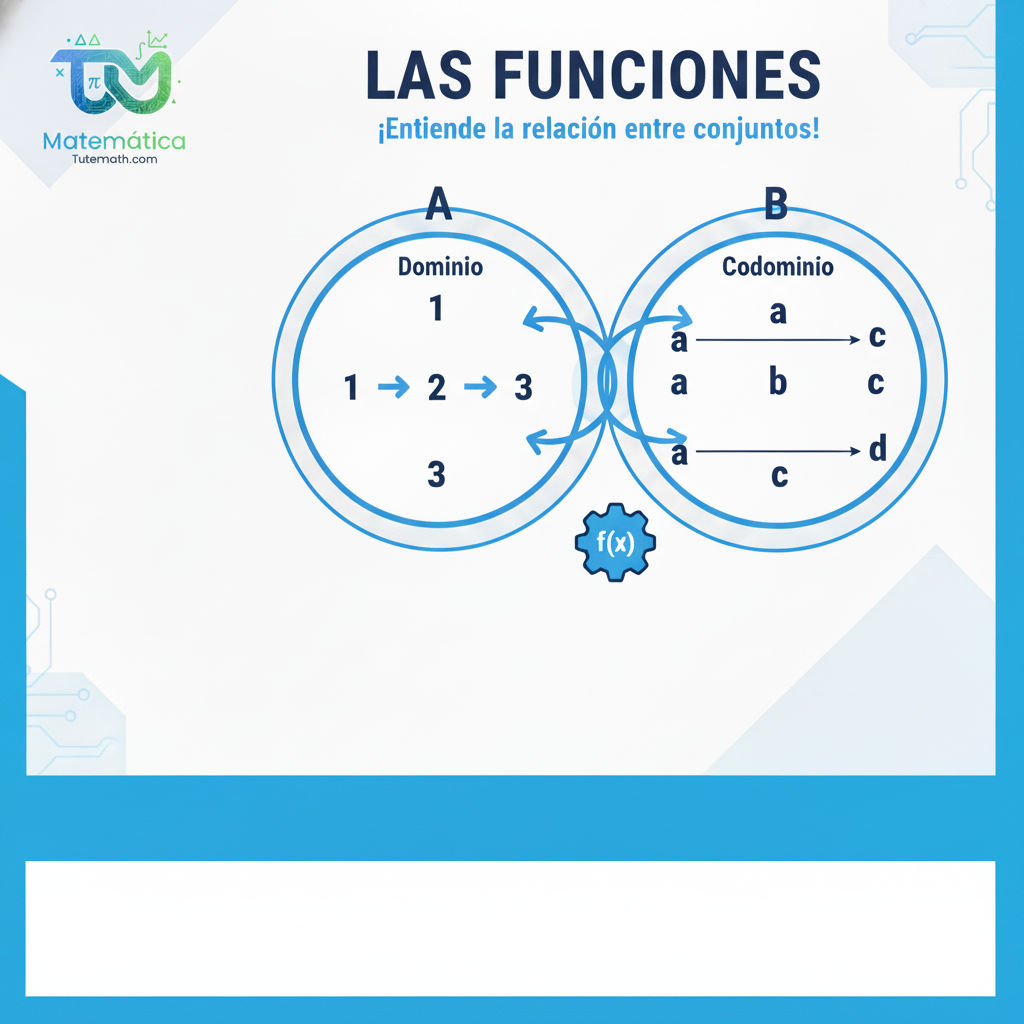
Una función es una relación especial entre dos conjuntos, que llamamos conjunto de partida (o dominio) y conjunto de llegada (o codominio).
Imagina que tienes una «máquina» matemática. Cada vez que le metes un elemento del conjunto de partida (la «entrada»), esta máquina te entrega exactamente un único elemento del conjunto de llegada (la «salida»).
Características clave de una función:
Todo elemento del conjunto de partida debe estar relacionado: No puede haber un elemento en el conjunto de partida que se quede sin «salida».
Cada elemento del conjunto de partida se relaciona con un único elemento del conjunto de llegada: Una «entrada» no puede tener dos «salidas» diferentes.
En la imagen, el conjunto A es el de partida (con elementos 1, 2, 3) y el conjunto B es el de llegada (con elementos a, b). Las flechas nos muestran cómo se relacionan: el 1 se relaciona con ‘a’, y el 2 se relaciona con ‘b’. Aquí es donde la imagen original presenta un detalle que podríamos mejorar o aclarar.
Enfoque
Hay dos enfoques para las funciones: el concepto Americano y el europeo.
En el concepto americano todos los elementos de un conjunto deben tener imagen.
En europeo admite que no todo elemento debe tener imagen, es lo que se conoce en América como una relación.
Funciones reales de variables reales.
Una función real de variable real denotada por f⊆RxR, es aquella que asigna a cada elemento del dominio un número real para obtener como imagen en el recorrido otro número real.
Campo de variación
Están referido a todo los elementos reales que pueden ser asignado a la variable independiente de manera que a la hora de aplicar la regla de correspondencia de la función la imagen obtenida no sea un numero imaginario o carente de sentido.
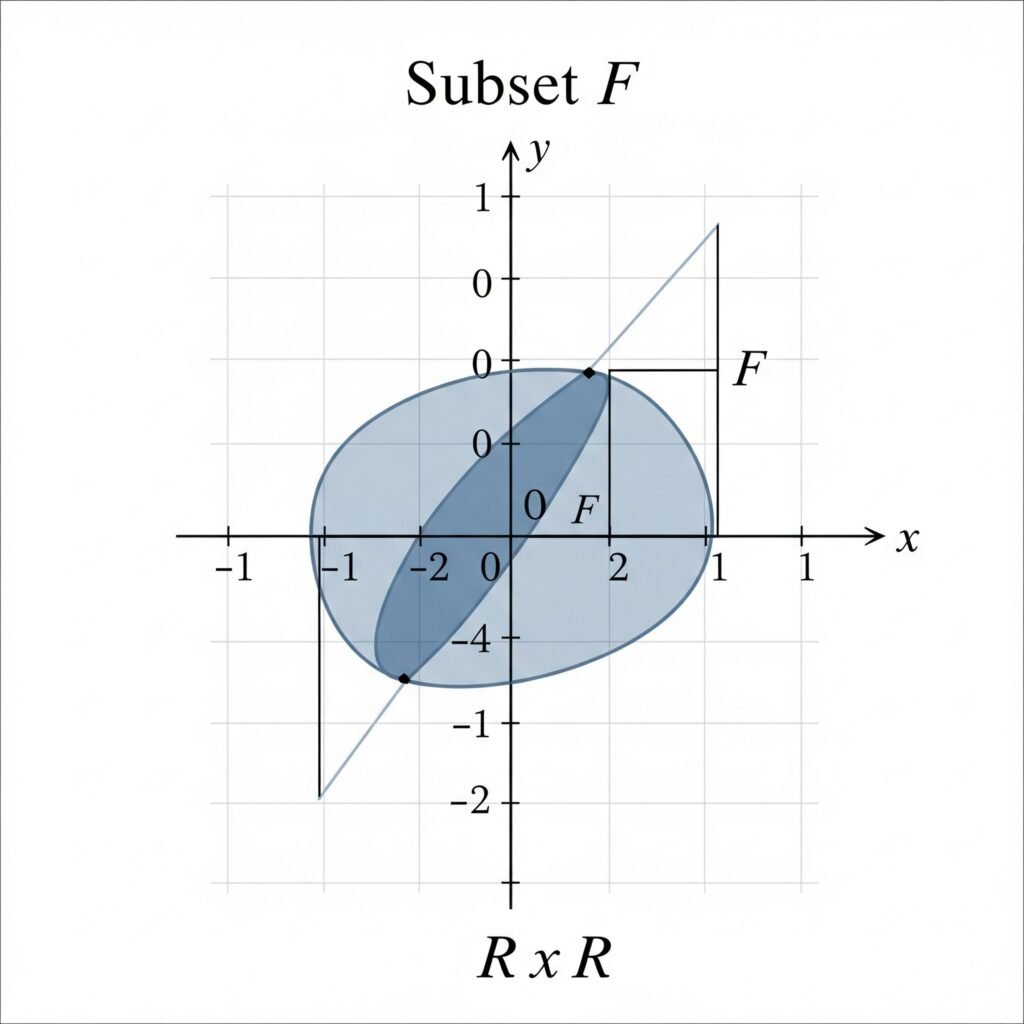

Ejemplo
xy-y-x=0
y=fx
Donde
y Es la variable independiente
fx Es la variable dependiente
Luego despejando y la cual es la variable independiente se obtiene
- el dominio de y
xy-y-x=0
xy-y=x
yx-1=x
y=xx-1
Restricciones
Dom y=xϵR ∀x≠1
- Ahora el recorrido
Recorrido de y entonces en este caso despeja x
xy-y-x=0
xy-x=y
xy-1=y
x=yy-1
Rec=yϵR ∀y≠1
Grafo de una función
El grafo de una función está constituido por un conjunto de pares ordenados px,y que satisface la regla de correspondencia de la función o ecuación. Sin embargo el grafo de una función está compuesto por infinitos pares ordenados.
Esto obliga a hacer una selección de los puntos más notables del grafo, acorde con la complejidad o dificultad de la función o ecuación.
Cuando se hace el grafo se debe acudir a algunas cualidades que poseen los grafos entre los que se destacan:
- El campo de variación
- El número de intercepciones o intersecciones lo cual se logra de la siguiente forma:
- Corta el grafo a y entonces y⇒x=0
y=f0
- El grafo corta a x⇒y=0
y=x2-7x+10
y=x-5x-2