TuTeMath — Matemáticas claras, paso a paso y sin estrés

Marco Teórico – Integrales Racionales

Marco teórico: Integrales racionales

Las integrales racionales son aquellas en las que el integrando se expresa como el cociente de dos polinomios. Su resolución depende principalmente del grado del numerador, del grado del denominador y de la factorización de este último.

Cuando el grado del numerador es menor que el del denominador y el denominador puede factorizarse en factores lineales o cuadráticos irreducibles, se utiliza el método de fracciones parciales. Este procedimiento permite descomponer la función racional original en una suma de fracciones más simples.

El fundamento teórico de las fracciones parciales se basa en que toda función racional propia puede expresarse como una combinación lineal de funciones elementales. Gracias a esta descomposición, una integral compleja se transforma en varias integrales básicas, facilitando su resolución.

El estudio de las integrales racionales es fundamental en el cálculo integral y tiene amplias aplicaciones en áreas como la física, la ingeniería y la economía.

Resolución de la Integral

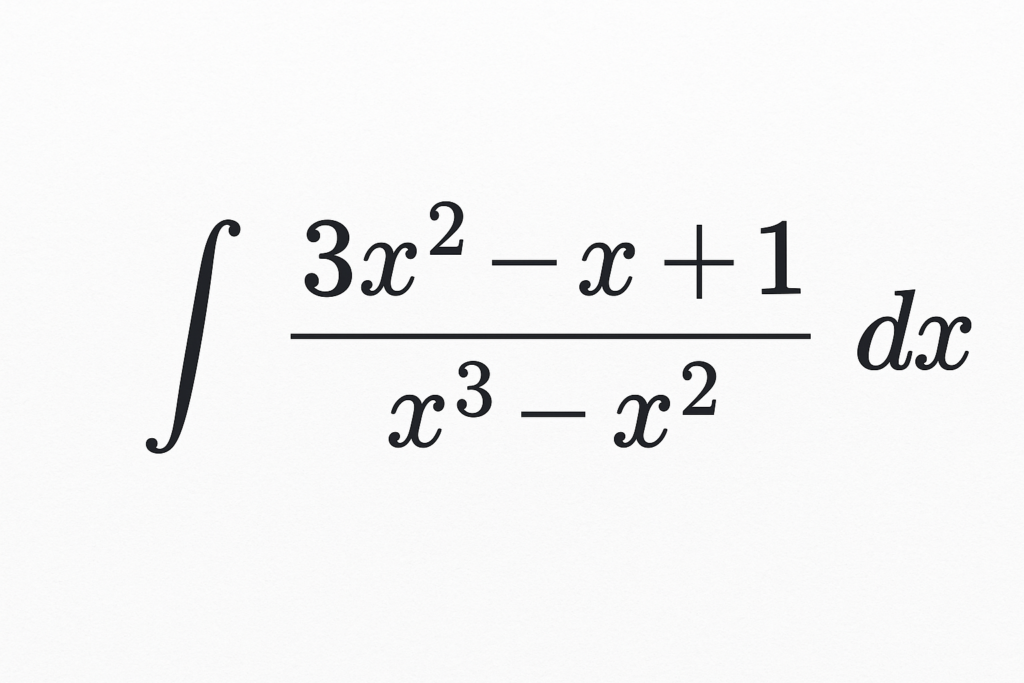
Integral original

∫ (3x² − x + 1) / (x³ − x²) dx

Paso 1: Factorización del denominador

x³ − x² = x²(x − 1)

Paso 2: Fracciones parciales

(3x² − x + 1) / [x²(x − 1)] = A/x + B/x² + C/(x − 1)

Paso 3: Igualación de coeficientes

A = 0
B = −1
C = 3

Paso 4: Sustitución

∫ [ −1/x² + 3/(x − 1) ] dx

Paso 5: Integración

∫ −x⁻² dx = 1/x
∫ 3/(x − 1) dx = 3 ln|x − 1|

Resultado final

1/x + 3 ln|x − 1| + C